');}

NOIP2013 普及组

Author Avatar
Actinoi 8月 16, 2019

T1:计数问题

题目描述

试计算在区间 1 到 n 的所有整数中，数字 x(0 ≤ x ≤ 9) 共出现了多少次？例如，在 1 到 11 中，即在 1,2,3,4,5,6,7,8,9,10,11 中，数字 1 出现了 4 次。

输入格式

2 个整数 n,x ，之间用一个空格隔开。

输出格式

1 个整数，表示 x 出现的次数。

输入输出样例

输入样例 #1

  1. 11 1

输出样例 #1

  1. 4

说明/提示

对于 100\% 的数据， 1≤ n ≤ 1,000,000,0 ≤ x ≤ 9 。

NOIP2013普及组第一题

题解：

​​​​ ​本题直接模拟就可以。在读入 n,\ x 之后，从 1\ \sim\ n 枚举数字，然后将枚举的数字的每一位与 x 进行比较，如果这一位等于 x 的话那么答案便 +1 。

  1. #include <iostream>
  2. using namespace std;
  3. int main() {
  4.     int n, x;
  5.     cin >> n >> x;
  6.     int ans = 0;
  7.     for (int i = 1; i <= n; i++) {
  8.         int p = i;
  9.         while (p > 0) {
  10.             if (p % 10 == x)
  11.                 ans++;
  12.             p /= 10;
  13.         }
  14.     }
  15.     cout << ans << endl;
  16.     return 0;
  17. }

T2:表达式求值

题目描述

给定一个只包含加法和乘法的算术表达式，请你编程计算表达式的值。

输入格式

一行，为需要你计算的表达式，表达式中只包含数字、加法运算符“ + ”和乘法运算符“ \times ”，且没有括号，所有参与运算的数字均为 0 到 2^{31}-1 之间的整数。

输入数据保证这一行只有 0-9 、 + 、 \times 这 12 种字符。

输出格式

一个整数，表示这个表达式的值。

注意：当答案长度多于 4 位时，请只输出最后 4 位，前导 0 不输出。

输入输出样例

输入样例 #1

  1. 1+1*3+4

输出样例 #1

  1. 8

输入样例 #2

  1. 1+1234567890*1

输出样例 #2

  1. 7891

输入样例 #3

  1. 1+1000000003*1

输出样例 #3

  1. 4

说明/提示

对于 30\% 的数据， 0≤ 表达式中加法运算符和乘法运算符的总数 ≤100 ；

对于 80\% 的数据， 0≤ 表达式中加法运算符和乘法运算符的总数 ≤1000 ；

对于 100\% 的数据， 0≤ 表达式中加法运算符和乘法运算符的总数 ≤100000 。

NOIP2013普及组第二题

题解：

​​​​ ​按照运算顺序，我们要先计算乘法，再计算加法。

​​​​ ​我的思路是首先算出所有乘法式子的值，然后再开一个 sum 数组来存储所有的值。最后，只需要将所有 sum 数组中的数字加起来就好了。

  1. #include <cstring>
  2. #include <iostream>
  3. using namespace std;
  4. long long sum[100001], k = 1;
  5. int main() {
  6.     string exp;
  7.     getline(cin, exp);
  8.     long long num = 0, all = 1;
  9.     for (long long i = 0; i < exp.length(); i++) {
  10.         if (exp[i] >= '0' && exp[i] <= '9') {
  11.             num = num * 10 + exp[i] - '0';
  12.         } else if (exp[i] == '*'){
  13.             all = (all * num) % 10000;
  14.             num = 0;
  15.         } else {
  16.             all = (all * num) % 10000;
  17.             sum[k] = all;
  18.             k++;
  19.             all = 1;
  20.             num = 0;
  21.         }
  22.     }
  23.     all = (all * num) % 10000;
  24.     sum[k] = all;
  25.     int ans = 0;
  26.     for (long long i = 1; i <= k; i++)
  27.         ans = (ans + sum[i]) % 10000;
  28.     cout << ans << endl;
  29.     return 0;
  30. }

T3:小朋友的数字

题目描述

有 n 个小朋友排成一列。每个小朋友手上都有一个数字，这个数字可正可负。规定每个小朋友的特征值等于排在他前面（包括他本人）的小朋友中连续若干个（最少有一个）小朋友手上的数字之和的最大值。

作为这些小朋友的老师，你需要给每个小朋友一个分数，分数是这样规定的：第一个小朋友的分数是他的特征值，其它小朋友的分数为排在他前面的所有小朋友中（不包括他本人），小朋友分数加上其特征值的最大值。

请计算所有小朋友分数的最大值，输出时保持最大值的符号，将其绝对值对 p 取模后输出。

输入格式

第一行包含两个正整数 n,p ，之间用一个空格隔开。

第二行包含 n 个数，每两个整数之间用一个空格隔开，表示每个小朋友手上的数字。

输出格式

一个整数，表示最大分数对 p 取模的结果。

输入输出样例

输入样例 #1

  1. 5 997 
  2. 1 2 3 4 5

输出样例 #1

  1. 21

输入样例 #2

  1. 5 7 
  2. -1 -1 -1 -1 -1

输出样例 #2

  1. -1

说明/提示

Case 1:

小朋友的特征值分别为 1,3,6,10,15 ，分数分别为 1,2,5,11,21 ，最大值 21 对 997 的模是 21 。

Case 2:

小朋友的特征值分别为 -1,-1,-1,-1,-1 ，分数分别为 -1,-2,-2,-2,-2 ，最大值 -1 对 7 的模为 -1 ，输出 -1 。

对于 50\% 的数据， 1 ≤ n ≤ 1,000,1 ≤ p ≤ 1,000 所有数字的绝对值不超过 1000 ；

对于 100\% 的数据， 1 ≤ n ≤ 1,000,000,1 ≤ p ≤ 10^9 ，其他数字的绝对值均不超过 10^9 。

NOIP2013普及组第三题

题解：

​​​​ ​对于每一个小朋友的特征值，就是求当前小朋友之前的最长公共子序列。无疑，读一个小朋友求一次最长公共子序列太浪费时间。因此，我们便可以设置一个 maxx 变量来记录当前小朋友之前的最长公共子序列。

​​​​ ​为了保证 maxx 不断更新，我们设置一个 s 数组，其中 s[i] 表示以 i 结尾的最长公共子序列。我们将新读进的数字计作 num ，考虑 s[i] 既可以作为一个子序列的起点，也可以接着之前的子序列继续延伸下去。因此 s[i]\ =\ max(num,\ num\ +\ s[i\ -\ 1]) ，所以 maxx 变量也就更新为 max\ (maxx,\ s[i]) ，这个小朋友的特征值 features[i] 也就是 maxx\ \%\ p 了。

​​​​ ​我们将 maxx 赋值为负无穷，来存储每个小朋友前面的所有人中，得分 + 特征值最高的那个数字。因此， maxx\ =\ max(maxx,\ features[i - 1]\ +\ score[i - 1]) ，同理，当前小朋友的得分也就等于 maxx 了。然后比较一下当前小朋友的得分是不是高于答案 ans ，若 score[i]\ >\ ans 的话， ans 更新为 score[i] 。最后，输出 ans 就OK辣！

  1. #include <iostream>
  2. using namespace std;
  3. long long features[1000001], score[1000001], s[1000001];
  4. int main() {
  5.     long long n, p, maxx = -2147483648, num = 0;
  6.     cin >> n >> p;
  7.     for (long long i = 1; i <= n; i++) {
  8.         cin >> num;
  9.         s[i] = max (num, num + s[i - 1]); //以 i 结尾的最长公共子序列
  10.         maxx = max (maxx, s[i]); // i 之前的最长公共子序列
  11.         features[i] = maxx % p;
  12.     }
  13.     long long ans = score[1] = features[1];
  14.     maxx = -2147483648;
  15.     for (long long i = 2; i <= n; i++) {
  16.         score[i] = maxx = max(maxx, features[i - 1] + score[i - 1]);
  17.         ans = max(maxx, ans) % p;
  18.     }
  19.     cout << ans << endl;
  20.     return 0;
  21. }

T4:车站分级

题目描述

一条单向的铁路线上，依次有编号为 1, 2, …, n 的 n 个火车站。每个火车站都有一个级别，最低为 1 级。现有若干趟车次在这条线路上行驶，每一趟都满足如下要求：如果这趟车次停靠了火车站 x ，则始发站、终点站之间所有级别大于等于火车站 x 的都必须停靠。（注意：起始站和终点站自然也算作事先已知需要停靠的站点）

例如，下表是 5 趟车次的运行情况。其中，前 4 趟车次均满足要求，而第 5 趟车次由于停靠了 3 号火车站（ 2 级）却未停靠途经的 6 号火车站（亦为 2 级）而不满足要求。

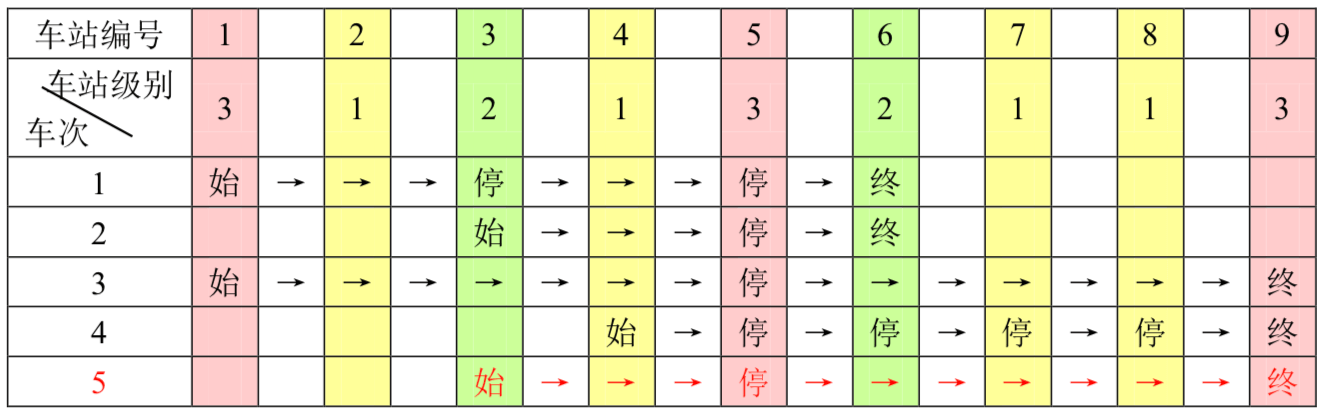
现有 m 趟车次的运行情况（全部满足要求），试推算这 n 个火车站至少分为几个不同的级别。

输入格式

第一行包含 2 个正整数 n, m ，用一个空格隔开。

第 i + 1 行 (1 ≤ i ≤ m) 中，首先是一个正整数 s_i(2 ≤ s_i ≤ n) ，表示第 i 趟车次有 s_i 个停靠站；接下来有 s_i 个正整数，表示所有停靠站的编号，从小到大排列。每两个数之间用一个空格隔开。输入保证所有的车次都满足要求。

输出格式

一个正整数，即 n 个火车站最少划分的级别数。

输入输出样例

输入样例 #1

  1. 9 2 
  2. 4 1 3 5 6 
  3. 3 3 5 6

输出样例 #1

  1. 2

输入样例 #2

  1. 9 3 
  2. 4 1 3 5 6 
  3. 3 3 5 6 
  4. 3 1 5 9

输出样例 #2

  1. 3

说明/提示

对于 20\% 的数据， 1 ≤ n, m ≤ 10 ；

对于 50\% 的数据， 1 ≤ n, m ≤ 100 ；

对于 100\% 的数据， 1 ≤ n, m ≤ 1000 。

NOIP2013普及组第四题

题解：

​​​​ ​这道题我们可以理解为凡是停靠过的站，那么这个站就比没停靠过的站级别高。

​​​​ ​因此，可以确定部分车站之间的两两大小关系，我们从级别低的车站 i 向级别高的车站 j 连边， topo[i][j] == 1 则代表 j 的级别比 i 的级别高。

​​​​ ​然后，怎么确定最少划分的级别数呢？这就需要 拓扑排序 了。

那么，啥是拓扑排序呢？

The canonical application of topological sorting is in scheduling a sequence of jobs or tasks based on their dependencies. The jobs are represented by vertices, and there is an edge from x to y if job x must be completed before job y can be started (for example, when washing clothes, the washing machine must finish before we put the clothes in the dryer). Then, a topological sort gives an order in which to perform the jobs.

（摘自维基百科）

​​​​ ​👆上面这段话说白了，就是如果干 y 工作之前必须先完成 x 工作（例如，你在烘干衣服之前必须要先把衣服洗干净，不然烘干也没用），而完成的这个顺序就是拓扑排序。

​​​​ ​因此，我们便可以利用拓扑排序的思想，不断删除停靠火车数为 0 的车站，然后把比这个车站高一级的所有车站 topo[i][j] 赋值为 0 ，将 j 车站中停靠的火车数 -1 ，最后输出一共执行了多少次操作就可以了。

  1. #include <cstring>
  2. #include <iostream>
  3. using namespace std;
  4. int st[1001], t[1001];
  5. int topo[1001][1001], level[1001]; //两站之间的拓扑序（若 topo[i][j] == 1 则代表 j 的级别比 i 的级别高）；每站的级别
  6. bool station[1001], cut[1001]; //判断本站有无火车停靠；是否已经删除这个点
  7. int main() {
  8.     int n, m;
  9.     cin >> n >> m;
  10.     
  11.     for (int i = 1; i <= m; i++) {
  12.         memset(station, false, sizeof(station)); //一开始没有任何火车停靠
  13.         int s;
  14.         cin >> s;
  15.         for (int j = 1; j <= s; j++) {
  16.             cin >> st[j];
  17.             station[st[j]] = true; // 表示本站有火车停靠
  18.         }
  19.         for (int j = st[1]; j <= st[s]; j++) { //枚举每个站点
  20.             if (station[j] == false) { //没有火车停靠本站点
  21.                 for (int k = 1; k <= s; k++) {
  22.                     if (topo[j][st[k]] == 0) {
  23.                         topo[j][st[k]] = 1; //k 的级别比 j 的级别高
  24.                         level[st[k]]++;
  25.                     }
  26.                 }
  27.             }
  28.         }
  29.     }
  30.     
  31.     memset(cut, false, sizeof(cut)); //一开始没有任何火车停靠
  32.     int ans = 0, top = 0;
  33.     
  34.     do { //不断删点、边
  35.         top = 0;
  36.         for (int i = 1; i <= n; i++) {
  37.             if (level[i] == 0 && cut[i] == false) { //这个车站的级别为 0 且没有删去这个点
  38.                 cut[i] = true;
  39.                 top++;
  40.                 t[top] = i;
  41.             }
  42.         }
  43.         for (int i = 1; i <= top; i++) {
  44.             for (int j = 1; j <= n; j++) {
  45.                 if (topo[t[i]][j] == 1) {
  46.                     topo[t[i]][j] = 0;
  47.                     level[j]--;
  48.                 }
  49.             }
  50.         }
  51.         ans++;
  52.     } while(top != 0);
  53.     
  54.     cout << ans - 1 << endl; // ans 会多加一次
  55.     return 0;
  56. }